A

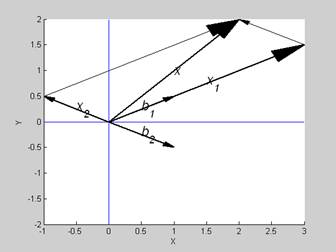
1) Množina B={(1, 0.5) ; (1, -0.5)}. Zistite či môže byť ortonormalnou bázou priestoru R² . (2B). Najdite k nej dualnu(biortogonálnu bázu) bazu. (2B). Ake súradnice má x(I)={2,2} v baze B? Zrekonstruujte ho a situaciu nakreslite. (4B)

a) B={(1,0.5);(1,-0.5)} je bazou (b1 a b2 su LNZ) ale nie ortonormalnou, neplati napr <m1, m1>=1;

b) Dualna Baza={(0.5,1);(0.5,-1)}

c) X(B)=B^(-1) X(I) = (3, -1)

Rekonstrukcia signalu, t..j znovuziskanie X(I) z sa da robit numericky
X(I) =B X(B)
a graficky

2) Nech G(t) = 4*t*F(6-2/t). Ak F(t) má nenulové hodnoty na intervale (1,3), kde ich ma G(t) ? (2B)

Treba pocitat, pre ake t ma vyraz (6-2/t) hodnotu 1 resp. 3. Takto dostaneme hladany interval (2/5, 2/3)

3) Akú hodnotu a_max (t.j. pri akom „a“ sú stredy elipsoidov) ocakavame pri analýze spojiteho skalogramu signálu X(t)=sin(4*t*pi) vytvoreného pouzitím waveletu so strednou frekvenciou 10Hz ?(2B)

Signal ma frekvenciu X(t)=sin(4*t*pi) 2Hz (je harmonicky a za sekundu ma dve periody), t.j. wavelet musime spomalit presne a_max=5 krat, aby sa maximalne zhodovali (=poloha stredu elipsoidov) .

4) Použite Haarovu MRA. Majme signál s(t), ktory vieme bezstratovo vyjadrit v priestore V_0. Pojekciami s(t) do priestorov sme získali súradnice c_1(n)={1,-1} a d_1(n) ={2,1}, kde n=1,2. Aká je príslužná aproximácia a detail signálu? (5B). Ako vyzera s(t)?(2B). Do akých priestorov V_m môžeme spravit projekciu s(t), aby nedošlo k strate informácie? (1B)

a) Pozor, c_1(n) a d_1(n) sú nenulové pre n=1,2

Musime ukazat ako vyzeraju funkcie

Aproximacia = F^_V_1(t) =sum_n( c_1(n) phi_(1,n)(t)

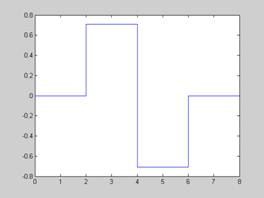
A

Detail = F^_W_1(t)=sum_n( d_1(n) psi_(1,n)(t)

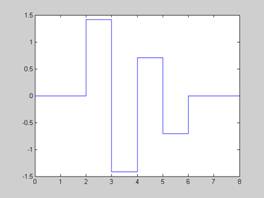
b) s(t) je ich suctom

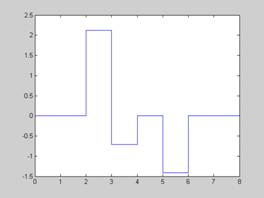
c) bezstratova projekcia je do V_m vsetkých lepsích ako pri m=0, t.j. m=-1, -2, …