Prva zapoctova pisomka – vysledky a riesenia
|
Os. Cislo |
Kruzok |
1.pisomka |
|
|
|
|
Body |
Skup. |
|
12328 |
2 |
19,00 |
B |
|
12309 |
2 |
19,00 |
A |
|
11527 |
2 |
19,00 |
A |
|
12349 |
1 |
18,50 |
A |
|
11019 |
1 |
18,00 |
A |
|
12323 |
3 |
18,00 |
B |
|
11525 |
2 |
18,00 |
A |
|
25290 |
3 |
17,50 |
A |
|
11596 |
1 |
17,00 |
A |
|
12335 |
1 |
17,00 |
A |
|
12270 |
3 |
17,00 |
A |
|
18800 |
3 |
17,00 |
A |
|
11108 |
3 |
16,50 |
B |
|
11101 |
3 |
16,50 |
B |
|
11813 |
1 |
16,00 |
B |
|
12315 |
2 |
16,00 |
B |
|
11574 |
2 |
16,00 |
A |
|
12274 |
2 |
16,00 |
B |
|
12275 |
2 |
14,50 |
B |
|
12322 |
3 |
14,00 |
B |
|
12310 |
2 |
14,00 |
B |
|
11564 |
2 |
14,00 |
A |
|
12342 |
1 |
12,00 |
B |
|
11572 |
2 |
12,00 |
A |
|
10424 |
3 |
11,00 |
B |
|
12338 |
1 |
10,00 |
A |
|
11667 |
3 |
10,00 |
B |
|
11105 |
3 |
10,00 |
B |
|
11829 |
3 |
9,00 |
A |
|
11733 |
3 |
9,00 |
B |
Riesenia:
A1)
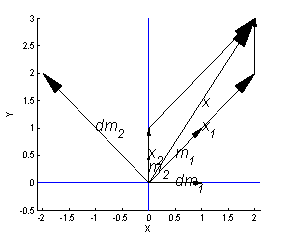
a) M={(1,1);(0,0.5)} je bazou (m1 a m2 su LNZ) ale nie ortonormalnou, neplati napr <m1, m1>=1;
b) Dualna Baza DB={(1,0);(-2,2)}
c) Rekonštrukcia signalu
X(M)={2,2} je znazornena:
A2) Problem je zistit ako su navzajom mapovane hodnoty G(x) = 8*F(y), v nasom pripade vieme x ale nevieme y. Staci dosadit za t prislusne hodnoty. Dostavame, ze F(t) je nenulove na intervale (4,5 ; 5,5).
A3) Pri t=0.5 ma argument hodnotu 2pi, t.j. s(t) ma frekvenciu 2
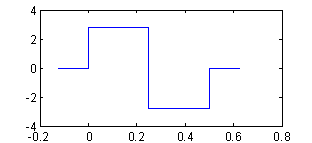
A4) Signál s(t), ma nenulove hodnoty na intervale (0, 0.5) a 4 koeficienty c_m(n)= (1, 1, -1,-1).
a) Phi trvalo teda ¼ z 0.5, t.j. 0.125s . Psi trva rovnako. Kedze pri m=0 trva Phi aj psi 1s, bolo ich treba 2^3 krat urychlit, t.j. m=-3
b) Rekonstruovane s(t) ma hodnoty +-2*sqrt(2), zobrazene je na obrazku.
c) Vhodnejšia voľba je m=-2, stačí to na náš signal. Úplne najlepšia voľba je m=-1. Tá tiež stačí.
B1)
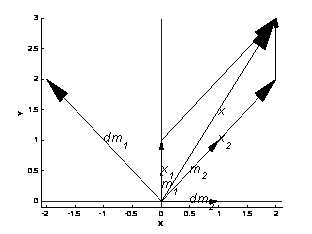
d) M={(0,0.5) ; (1,1) } je bazou (m1
a m2 su LNZ) ale nie ortonormalnou,
neplati napr <m1, m1>=1;
e) Dualna Baza DB={(-2,2), (1,0)}
f)
Rekonštrukcia
signalu X(M)={2,2} je znazornena:
B2) Problem je zistit ako su navzajom mapovane hodnoty G(x) = 5*F(y), v nasom pripade vieme x ale nevieme y. Staci dosadit za t prislusne hodnoty. Dostavame, ze F(t) je nenulove na intervale (4,5 ; 5,5).
B3) Pri t=1 ma argument v sinuse hodnotu 2pi, t.j. s(t) ma frekvenciu
1
B4) Signál s(t), ma nenulove hodnoty na intervale (1, 2) a 4 koeficienty c_m(n)= (1, 1, -1,-1).
a) Phi trvalo teda ¼ z (2s-1s), t.j. 0,25s . Psi trva rovnako. Kedze pri m=0 trva Phi aj psi 1s, bolo ich treba 2^2 krat urychlit, t.j. m=-2
b) Rekonstruovane s(t) ma hodnoty +-2, zobrazene je na obrazku.
c) Vhodnejšia voľba je m=-1, stačí to na náš signal. Úplne najlepšia voľba je m=0. Tá tiež stačí.
