Link Reversal Routing Algoritmus (LRR)
Obsah
Úvod
Link Reversal (neskôr len LR) poskytuje jednoduchý mechanizmus na smerovanie komunikácie v sieťach s často sa meniacou topológiou, ako sú napríklad ad-hoc mobilné siete. LR smeruje predkladaním smeru komunikácie na každej linke siete čoho výsledný graf je cieľovo orientovaný DAG (Directed Acyclic Graph). Jednou zo základných kritérií je znižovanie informácií prenášaných medzi uzlami siete pri zmenách siete. V prípade, že uzol stratí komunikačnú cestu k cieľu, táto situácia sa rieši presmerovaním jednej alebo všetkých súvisiacich spojení s porušenou komunikačnou cestou. LR ako samostatný algoritmus bol testovaný experimentálne a jeho praktické využitie sa našlo v algoritmoch ako sú TORA, Gafni-Bertsekas algoritmus (G-B), LMR, atď.
Pre úplnosť informácií je potrebné spomenúť dve varianty LR – a to s úplným spätným algoritmom a s čiastočným spätným algoritmom. Úplný LR v porovnaní s čiastočným LR je jednoduchší pričom jeho výpočtová náročnosť sa dá vyjadriť ako O(n2) kde n je počet uzlov, ktoré stratili destináciu. Náročnosť čiastočného LR sa dá vyjadriť ako O(n . a* + n2) kde a* je nenulová veličina priamo súvisiaca so stavom siete. Na počiatočné ustabilizovanie je potrebné Ω( n2) operácii ako aj času. Z tohto dôvodu môžeme povedať, že úplný LR je výhodnejší použiť pri najhorších možných schémach keďže čiastočný LR môže svojvoľne narastať.
Funkčnosť algoritmu je vysvetlený na sieti kde topologická zmena priviedla sieť do stavu, kde uzly stratili svoje prenosové cesty k cieľu. Vid diagram pre čiastočný LR a úplný LR.
Na nasledovných podmienkach môžeme sledovať ako sa správa celý systém keď sieť sa dostáva do stavu kedy jednotlivé uzly stratili svoje cesty k určitým cieľom. Takémuto stavu sa v odbornej terminológii hovorí „počiatočný stav siete“. V momente kedy sa už v sieti nedejú ďalšie topologicé zmeny sa sieť stabilizuje a nastaví sa znova do smerovo orientovaného módu ( inými slovami dosiahne konečný stav).
V tomto prípade analyzujeme 2 parametre:
- Práca: Počet uzlových zmien( nod reversals) k dosiahnutiu stabilizácie – uzlová zmena je operácia pri ktorej doslovne potopí niektoré zo všetkých priľahlých spojení. Týmto spôsobom sa zisťuje sila a výpočtová náročnosť potrebná algoritmom ako reakcia na topologicé zmeny.
- Čas: Počet paralelných krokov k dosiahnutiu stabilizácie, čo je parameter merania rýchlosti a reagovania algoritmu na vzniknuté topologicé zmeny. V tomto zjednodušenom modeli sa každá zmena (reversal) počíta ako jeden krok (v časovej oblasti) pričom sa zmeny môžu objaviť v rovnakom časovom intervale bez hocijakých obmedzení. Zmeny využívajú váhový model. RA (reversal algorithm – algoritmus zmeny) pridelí váhu každému uzlu siete. Spojenie je orientovane zásadne z uzla s väčšou váhou k tým s menšou. Potopenie spojenia zvýši váhu o rozumnú hodnotu čo vedie k preorientovaniu spojenia niektorých alebo všetkých spojení. Berieme LR ako deterministický algoritmus v ktorom potopenie zvyšuje jeho váhu podľa deterministickej funkcie prislúchajúcej k aktuálnej hodnote váhy konkrétneho a všetkých susediacich uzlov. G-B algoritmus je deterministický.
V analýze delíme uzly na dobé a zlé. Za zlý uzol považujeme taký z ktorého nepokračuje cesta do cieľa. Každý iný uzol obsahujúci cieľ považujeme ako dobrý. Je potrebné si uvedomiť že uzol, ktorý neposkytuje cestu k cieľu má automatický potopené spojenie. Na nasledovnej ukážke je možné vidieť výsledky jednotlivých algoritmov.
Úplný LR
Pri úplnom LR je ukázané ako zo začiatočného stavu s n zlými uzlami
sa stabilizuje po výpočtovej práci a čase rovnajúcej sa O(n2).
Výsledky pre LR sú omnoho lepšie. Je možné každú sieť rozdeliť pričom
sa berie ohľad na zlé uzly. Z tohto stavu každý výpočtový úkon
vykonaný uzlami dá predpovedať v závislosti od poriadia
vykonávania. Uzol v j-tej vrstve prevedie zmenu presne j krát
kým sa stabilizuje. (vid. obr. č. 2)
diagram
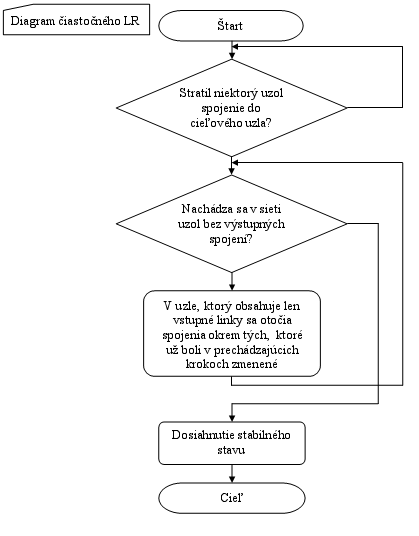
Čiastočný LR
Pri
čiastočnom LR je ukázané ako zo začiatočného stavu s n zlými
uzlami sa stabilizuje po výpočtovej práci a čase rovnajúcej sa
O(n . a* + n2), čo korešponduje s rozdielom
maximálnych a minimálnych váh uzlov v počiatočnom stave.
(vid. obr. č. 1)
diagram
Deterministický algoritmus
V rámci
deterministického „reversal“ algoritmu je možné z grafu
vyčítať, že sa vychádza z počiatočných podmienok pričom každý
zlý uzol nachádzajúci sa d skokov od najbližšieho dobrého uzla
musí vykonať d zmien na dosiahnutie stabilného stavu.
Je dokázané že existujúce siete z počiatočného stavu s n
zlými uzlami využívajúc algoritmus potrebujú (n2) operácií
a časových sekvencií k dosiahnutiu stabilného stavu. Ako
dôsledok odvíjajúci sa od najhoršej možnej schémy úplný LR je
časovo a výpočtovo optimálnejší v porovnaní s čiastočným
LR.
Ekvivalencia vykonávania
Ako je dokázané, že pre hociktorý „reversal“ algoritmu distribuované operácie algoritmu štartujúce z rovnakého počiatočného stavu sú ekvivalentné: 1) konečný stav siete po dosiahnutí stabilizácie je vždy rovnaký a 2) každý uzol vykoná rovnaký počet zmien na dosiahnutie stability pri všetkých vykonaniach. Vyplývajúc z tohto faktu algoritmus je nezávislý na poradí
Zoznam literatúry
[1] Analysis of Link Reversal Routing Algorithms http://polaris.cse.fau.edu/~jie/teaching/fall_2004_files/reversal2.ppt
[2] Analysis of Link Reversal Routing Algorihms for Mobile Ad Hoc Networks http://dcg.ethz.ch/lectures/ws0405/seminar/materials/born_slides.pdf
[3] Link Reversal Routing (LRR) in Ad-Hoc Networks http://comet.ctr.columbia.edu/~jaekwon/E6768/Andreas-EE6768project1.pdf
[4] Ad Hoc http://en.wikipedia.org/wiki/Ad-hoc
[5] The SECAN-LAB: Gafni-Bertsekas http://wiki.uni.lu/secan-lab/Gafni-Bertsekas.html
[6] The SECAN-LAB: Lightweight Mobile Routing http://wiki.uni.lu/secan-lab/Lightweight+Mobile+Routing.html